[빅데이터분석기사] 교차분석(Cross-tabulation Analysis)
교차분석(Cross-tabulation Anlaysis)
비교 대상이 되는 항목들의 빈도를 이용하여 자료 간 관계의 유의성을 파악할 때 사용한다. 주로 '범주형' 자료 간의 관계를 확인하는 데 쓰이며, 전체 비율을 통해 예상빈도를 구하여 실제빈도와의 차이를 대조하는 방식이다.
아래는 당뇨환자 25명과 당뇨가 없는 정상인 75명의 인원 총 100명의 비만 유무를 조사한 결과이다. 100명 가운데 비만(20)과 정상(80) 체중의 구성비가 1:4이므로 당뇨환자군 안에서 비만과 정상의 비율 역시 1:4, 비환자군 안에서도 1:4의 비율로 환자 수가 도출될 것을 예상해 볼 수 있다. 이를 기대빈도(예상빈도)라 한다.

당연히 실제로 빈도수는 예상과 다를 것이다. 관측빈도 부분을 보면 당뇨환자 25명 중 비만인 사람은 10명, 정상체중인 사람은 15명으로 실제는 2:3의 구성비를 나타냈고, 당뇨병이 없는 정상 범주의 인원 75명 중 비만인 사람은 10명이고 정상체중인 사람은 65명으로 약 1:6:5 비율이 확인됐다.
여기서 한 가지 유념해야 할 내용은 바로 변수의 개수이다. 얼핏 변수의 개수가 4개(2*2)로 보일 수 있지만 여기서 변수는 2개다. 첫 번째 변수는 당뇨환자와 정상인의 범주 정보가 되고, 두 번째 변수는 비만체중과 정상체중의 범주 정보가 되는 것이다. 변수의 개수는 가설검정 시 자유도 선택에 영향을 주므로 확실히 해야 한다.
비만과 체중의 교차분석에 대한 카이제곱 검정
범주형의 자료를 바탕으로 교차분석을 실시했을 때 우리는 '카이제곱(x^2) 검정'을 사용해 분석 결과가 통계적으로 유의미한 것인지 그저 우연인 것인지 확인해 볼 수 있다.
| 귀무가설 H0 | 두 변수는 연관성이 없다 |
| 대립가설 H1 | 두 변수는 연관성이 있다 |
분포표를 확인하면, 자유도가 1일 때 카이제곱 검정 통계량이 3.84보다 작아야 유의수준(P-value)이 0.05이하가 되어 귀무가설을 기각(=대립가설을 채택)하게 된다.

카이제곱 검정 통계량은 아래 계산식에서 8.33이고, 유의수준이 0.004로 확인됐다. 통계량이 거의 0에 가까우므로 앞선 교차분석에 사용된 두 변수 간 유의성은 상당하다고 할 수 있다.

정리하면, 카이제곱 분포표를 보는 방법은 다음과 같다. 분포표에서 자유도와 유의수준을 기준으로 우리가 확인할 기준값(Threshold)을 찾는다. 본 예제에선 관계를 밝힐 변수의 수가 2개이므로 자유도가 1(=(2-1)*(2-1))이고 유의수준을 0.05로 설정했으므로 기준값은 3.84가 된다.
더불어 카이제곱 검정 통계량은 공식에 따라 8.33이 나왔다. 그러므로 유의수준 0.05에서 귀무가설을 기각할 수 있다고 결론낼 수 있다. 더 나아가 8.33은 6.63의 P-값이 0.01인 경우보다 훨씬 큰 값이다. 유의수준이 거의 0에 수렴한다는 사실을 알 수 있다. 따라서 두 변수는 서로 독립적이지 않고 서로 밀접한 영향을 미친다고 해석할 수 있다.
카이제곱 통계량과 분산의 개념, 결국 평균으로부터의 거리를 구한 것!
앞서 관측빈돗값에서 기대빈돗값을 빼고 제곱한 값을 모두 더한 공식을 통해서 우리는 앞서 배운 분산을 떠올려야 한다(뒤에서 다룰 최소제곱법도 함께 이해하면 좋다). 분산의 공식을 다시 확인하면, '편차 제곱의 합'이다. 해당 수식을 통해서 분산은 데이터의 변동성을 설명했다. 자료의 개수로 평균으로부터의 거리 합을 나누었으니 데이터가 얼마나 퍼져있을지를 뜻하는 것이다.

같은 방식의 카이제곱 검정 통계량은 어떤가. 기대빈도수를 기준으로 실젯값과 기댓값의 차이를 양수적(제곱)으로 표현하겠다는 의도를 수식 안에 넣어 놓았다. 관측빈도는 실 데이터의 값이고 기대빈도는 전체 비율에 근사하게 얻은 일종의 평균이다. 더불어 관측빈도와 기대빈도의 차이를 양수화(제곱)하고 그것을 평균으로 다시 나눴다. 그 의미는 기대빈도로부터 관측 결과가 얼마나 떨어져있는가(=거리)를 확인하고 있다. 그렇다면 분자의 값이 크면 클수록 거리가 멀다는 의미와 같고 거리가 멀다는 것은 곧 예측치와 관측치의 차이가 크다는 것을 의미한다. 결국 카이제곱 통계량은 교차 확인한 변수들이 서로 얼마나 먼지 또는 가까운지를 설명하는 수치인 셈이다.
분석 연습
슬관절염으로 청구된 연령별 분포를 가지고 교차분석을 실시한다. 분포 연령대는 20년 등간(0~10, 20~30, 40~50, 60~70, 80대~) 구분을 두었다. 2020년 12월 연령대별 전체 청구명세서 건수와 그 가운데 슬관절염이 주·부상병인 청구명세서 건수를 분석 대상으로 하고 있다.
DATASET
2020년 12월, 연령대별 전체 청구명세서 건수
2020년 12월, 연령대별 슬관절염이 주·부상병인 청구명세서 건수
1) 청구명세서 건수를 5개의 연령별 범주로 나누어 각 연령대별로 슬관절염이 얼마만큼의 비중을 갖는지 교차표를 작성한다. 젊은 연령일수록 슬관절염 관련 청구량 비중이 매우 낮다는 사실을 확인할 수 있다.

2) 전체 청구명세서 가운데 슬관절염의 발병 실제빈도가 얼마나 유의한 것인지(=우연한 것이 아닌지) 확인하기 위해 귀무가설과 대립가설을 설정한다.

3) 전체 청구명세서 중에서 슬관절염으로 청구한 명세서 건수의 비중을 파악한다. 슬관절염 관련 청구 빈도를 바탕으로 연령별 기대빈도를 확인한다. 전체 슬관절염 건수를 각 연령마다 곱해 기댓값을 구하였다.

4-1) 80대 이상 연령대의 슬관절염 건수 기대수준과 실제빈도가 가장 높다. 해당 값이 얼마나 통계적으로 유의한 값인지 실제 데이터로 카이제곱 검정을 통해 확인한다. (범주형 자료를 분석한 결과에 대한 검정의 기준값은 카이제곱 분포(표)를 참조한다). 빈도를 바탕으로 연령별 기대빈도를 확인한다. 전체 슬관절염 건수를 각 연령마다 곱해 기댓값을 구하였다.

4-2) 자유도 확인 : 자료 범주를 연령대별 5개 구간을 설정하였으므로 변수 x의 수는 5개가 되고 자유도는 여기서 5-1한 '4'가 된다.
4-3) 기준값 확인 : 자유도 4, 유의수준 0.05를 기준으로 빈돗값의 유의성을 판단할 기준을 찾는다.
4-4) 관측 데이터를 카이제곱 검정 함수에 넣어 반환되는 통계량을 확인한다.
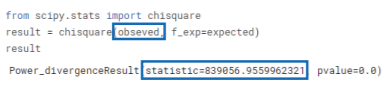
5) 마지막으로 앞서 확인했던 기준값인 9.49 이내로 해당 통계량이 들어오는지 확인한다. 기준을 넘지 않으면 대립가설을 채택하여 슬관절염 청구 건은 연령과 관계가 있다고 결론내린다.