[빅데이터분석기사] 최근접 이웃(K-Nearest Neighbors)
최근접 이웃
알고리즘은 우리가 예측하려고 하는 임의의 데이터와 가장 가까운 데이터 K개를 찾아 다수결에 의해 데이터를 예측하는 방법이다.

위 그림과 같이 두 그룹의 데이터가 있을 때 주어진 임의의 데이터가 어느 그룹에 속할 것인지를 K-NN 알고리즘으로 풀 수 있다. 별 데이터로부터 가장 가까운 K개 데이터들이 더 많이 속한 그룹으로 별 모양 데이터를 분류하는 알고리즘이다. K가 3이라면 3개의 데이터를 확인해 더 많은 데이터가 있는 B그룹으로 주어진 임의의 데이터를 분류한다. K의 선택 기준은 학습의 난이도와 데이터의 개수이며, 보통 훈련 데이터 개수의 제곱근으로 설정한다.
K와 별 모양 데이터 간 좌표상 거리도 고려해야 한다. K를 4로 설정했다면 별 모양 데이터를 기준으로 4개의 데이터 간 떨어진 거리가 다르다. 별 모양 데이터를 기준으로 파란 데이터 중 1개 데이터의 거리가 가장 멀어 가중치가 가장 낮으므로 B그룹으로 분류된다.
K-NN의 장단점
K-NN 알고리즘의 장점은 추가된 데이터의 처리가 쉽고, 예측 결과에 대한 해석도 쉽다는 것이다. 사용이 간단하여 훈련 데이터에 대한 훈련 과정이 별도로 필요하지 않으며, 범주를 나눈 기준을 알지 못하더라도 데이터를 분류할 수 있다.
반면 훈련 데이터 세트의 크기가 너무 크거나 특성(feature)의 개수가 너무 많으면 연산속도가 느려지는 단점이 있다. 비수치 데이터의 유사도를 정의하기가 어렵고 이상치의 영향을 크게 받는다. 서로 다른 특성값들의 비율을 일정하게 하지 않을 경우 성능이 떨어지기 때문에 같은 스케일(규모)을 갖도록 전처리 하는 과정이 필수적이다.
최근접 이웃을 활용한 회귀분석 사례
지도학습 방법으로 클래스가 정해진 데이터에 대해 분류 모델을 만들어 분류예측에 사용하거나 최근접 이웃 회귀분석에도 사용할 수 있다.
K값이 너무 작으면 거리가 가장 가까운 데이터 1개를 기준 삼아 새로운 데이터를 분류하게 되므로 분류 기준이 매우 엄격해진다. 훈련 데이터 세트에 대해서는 높은 정확도를 기대할 수 있지만 임의의 테스트 데이터 세트에는 높은 정확도를 기대하기 어려워진다. 결과적으로 과대적합(overfitting) 문제가 발생할 수 있다.
K값이 너무 크면 거리가 가장 가까운 K개의 모든 데이터를 기준으로 데이터를 분류하기 때문에 모델의 분류 기준이 매우 모호해진다. K가 극단적으로 커질 경우 훈련 데이터에 대해서 정확도 성능이 나오지 않는 과소적합(underfitting) 문제가 생길 수 있다.

따라서 최근접 이웃 알고리즘을 사용할 때는 적절한 K의 개수를 정하는 것이 매우 중요하다. 일반적으로 K-NN 분류 모델을 훈련시킬 때 일정 범주를 주고 학습을 시키며, 교차검증이나 리샘플링 기법을 이용하여 최적의 성능을 내는 K 값을 구한다.
DATASET
National Institute of Diabetes and Digestive and Kidney Diseases에서 제공된 당뇨병 진단 장치로부터 나온 데이터와 당뇨병의 여부를 보여준다. 샘플의 개수는 총 768개이고 21세 이상의 여성이다. 데이터 특성(feature)은 임신횟수, BMI, 인슐린 Level, 나이 등이 있으며, 결과는 당뇨병의 여부(0, 1)로 표현되어 있다.
1) 데이터 확인하기
df = pd.read_csv('./diabetes.csv')
df.head()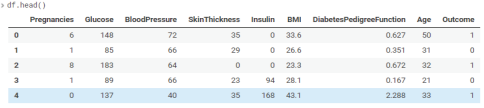
2) 훈련, 시험 데이터 분할(6:4)
X_train, X_test, y_train, y_test = train_test_split(X_rescale, y, test_size=0.4, random_state=42, stratify=y)3) K값을 변경하면서 알고리즘 정확도 측정
neighbor = np.arange(1, 9)
train_accuracy = np.empty(len(neighbors))
test_accuracy = np.empty(len(neighbors))
for i, k in enumerate(neighbors):
#Setup a knn classifier with k neighbors
knn = KNeighborsClassifier(n_neighbors=k)
#Fit the model
knn.fit(X_train, y_train)
#Compute accuracy on the training set
train_accuracy[i] = knn.score(X_train, y_train)
#Compute accuracy on the test set
test_accuracy[i] = knn.score(X_test, y_test)
4) 훈련 데이터와 시험 데이터 정확도의 차이가 가장 작은 K=7인 값을 이용하여 정확도 측정
confusion_matrix(y_test, y_pred)
pd.crosstab(y_test, y_pred, rownames=['실제'], colnames=['KNN모델'], margins=True)
민코프스키 공식을 이용한 K-NN의 거리측정
knn = KNeighborClassifier(n_neighbors=k, p=2, metric='minkowski')최근접 이웃 알고리즘에서 사용되는 데이터 간 거리를 구하는 방식에는 '맨해튼'과 '유클리드' 측정 방식이 있다. 맨해튼 거리 측정 방식은 두 점 사이의 격자를 고려한 거리 측정 방식이고, 유클리드 거리 측정 방식은 최단거리를 측정한 것이다. 다음은 맨해튼과 유클리드 거리를 나타낸 그림과 공식이다.


민코프스키 공식은 거리를 구하는 공식을 일반화해 놓은 것이며, 위 식과 같다. 이때 P=1이면 맨해튼 거리, P=2일 때 유클리드 거리를 계산한다. 파이썬의 KNeighborsClassifier 함수에서 인자값을 생략 할 경우, 민코프스키에 P=2(유클리드 거리)가 기본값으로 설정되어 있다.
함께 보면 좋은 글
[빅데이터분석기사] 의사결정나무(Decision Tree)
[빅데이터분석기사] 의사결정나무(Decision Tree)
의사결정나무 일종의 분류 기법이다. 전체 집단을 계속 양분하는 분류기법으로써 분기가 발생하는 포인트(=노드)에는 기준이 되는 질문이 있어 기준 질문에 부합하냐(YES), 부합하지 않느냐(NO)에
it-utopia.tistory.com
[빅데이터분석기사] 랜덤포레스트(Random Forest)
[빅데이터분석기사] 랜덤포레스트(Random Forest)
랜덤포레스트(RF) 의사결정나무를 여러개 모아서 데이터 분류 및 예측을 수행하는 AI알고리즘이다. 어떤 데이터 집단에 대한 분류나 예측을 실시한다고 할 때, 하나의 결정트리를 사용하는 것보
it-utopia.tistory.com
[빅데이터분석기사] 앙상블(Ensemble)
앙상블 학습(Ensemble Learning) 그동안 우리는 여러 기계학습 모델들을 살펴보았다. 이렇게 개별적으로 동작하는 모델들을 모아 종합적으로 의사결정을 한다면 어떨까? 앙상블은 프랑스어로 전체적
it-utopia.tistory.com
[빅데이터분석기사] 서포트벡터머신(SVM)
서포트벡터머신(SVM) 분류를 위한 기준선을 정의하는 모델이다. 분류되지 않은 새로운 점이 나타나면 어느 쪽에 속하는지 확인을 위해서 결정 경계를 정한다. 데이터에 2개 속성(feature)만 있다면
it-utopia.tistory.com
[빅데이터분석기사] 군집분석(Clustering Analysis)
[빅데이터분석기사] 군집분석(Clustering Analysis)
군집분석 분류 기준이 없는 상태에서 데이터 속성을 고려해 스스로 전체 데이터를 N개의 소그룹으로 묶어내는(Clustering) 분석법이다. 유사성이 높은 대상 데이터를 묶고, 서로 다른 그룹에 속한
it-utopia.tistory.com