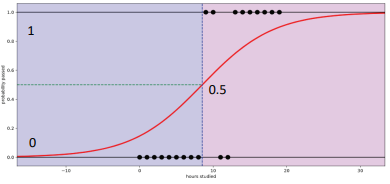
시계열분석 시간에 따라 변화되는 자료의 패턴을 밝혀 가까운 미래를 예측하는 방법이다. 시계열분석을 위해서는 시계열 데이터가 준비돼야 한다. 시간의 경과만 한 축(x)을 구성하는 것이 아니라 시간 경과가 일정한 시차로 정돈되어 있을 때 이를 시계열 데이터로 본다. 시계열 데이터의 필수 조건, 정상성(Stationary) 정상성이란 '데이터 변동의 안정성'으로 달리 표현할 수 있다. 시간의 흐름에 따라 관측된 결과에서 세로축(y) 값의 변동이 지나치게 크다면 그 다음 예측에 관한 정확도가 높을 수 있을까? 그렇지 않을 것이다. 회귀분석에서 살펴보았듯이, 데이터의 분포가 추세선을 기준으로 잘 모여 있을 때(=표준오차가 작을 때), 해당 추세선이 보다 예측력이 높다고 배웠다. 마찬가지로 어떤 시계열 자료가 정확..