회귀분석
일반적으로 예측을 목표하는 통계 분석이다. 예측을 하는 방법에 핵심이 되는 개념이 바로 '추세선'이다. 좌표상에서 데이터의 분포와 앞으로의 변화를 가장 잘 설명할 수 있는 하나의 선을 그려내는 것이 회귀분석의 궁극적인 목적이 된다.

추세선의 의미
직선의 추세선을 수식으로 표현하면, y=ax+b와 같은 1차 방정식이 된다. 여기서 x와 y는 이미 알고 있는 데이터값이다. 여기서 수식을 활용해 데이터 변화의 추세를 확인하는 방법은 x와 y에 들어오는 값을 기준으로 해당 수식을 충족시키는 a(=기울기), b(=절편) 값을 찾는 것이다. 즉, 추세선을 통한 회귀적 예측이란 곧 a, b를 구하는 과정을 말하는 것이다. 여기서 a와 b를 '회귀계수'라 한다.

회귀의 시작, 최소제곱법(=최소자승법 Ordinary Least Squares)
그렇다면 최적의 회귀계수 a와 b를 어떻게 찾을 수 있을까. 이 떄 사용되는 개념이 최소제곱법이다. 최초엔 임의의 추세선(=가설초기화)을 기준으로 분포한 x,y의 좌푯값의 차이(=잔차)를 제곱하여 모두 더한 값이 최소가 되는 지점들을 연결하는 방법이다.
잔차가 최소인 부분을 찾는 이유는 잔차가 곧 '오차'를 의미하기 때문이다. 추세선을 기준으로 실제 분포한 좌푯값과의 거리가 크다면 오차가 큰 것이다. 오차는 추세선보다 클 수(+)도 있고 작을 수(-)도 있다. 값의 크기와 관계없이 차이에 대한 절댓값(=거리)을 필요로 하므로 오차마다 제곱을 하게 되고 그 값들의 합이 최소가 될 때 비로소 추세선과 데이터값과의 오차의 합이 가장 작아지게 된다.
따라서 OLS는 잔차들의 제곱합 값이 가장 작은 값의 선분을 찾아감으로써 평균으로 '회귀'하는 성질을 가지며, 우리는 이를 활용해 회귀적인 분석(예측)을 할 수 있다.

추세선은 얼마나 정확한 것일까, 표준오차와 회귀계수
데이터가 다르더라도 동일한 방정식과 회귀계수를 가질 수 있다. 이런 경우 표준오차의 차이를 확인하여 구분해 볼 수 있다. 표준오차란 회귀선(=추세선)과 데이터 간 차이의 표준값이다. 표준편차는 데이터와 평균간 표준 거리 차였고, 표준오차는 회귀(직)선을 기준으로 데이터가 얼마나 잘 모여있거나 퍼져있는지를 표현한 개념이다. 따라서, 아래 그림과 같이 표준오차(SE)가 작다면 회귀선 주변에 가깝게 데이터가 분포하고 있음을 뜻하고, 반대라면 회귀선으로부터 데이터가 멀리 퍼져있음을 의미한다.
정리하면, 회귀선을 기준으로 데이터가 잘 모여 있다는 말은 다른 말로 해당 추세선이 데이터를 잘 설명해준다는 말이며 이는 곧 표준오차가 작다는 말과 동치이다. 그러므로 회귀계수(y=ax+b)를 구했을 때 표준오차가 큰 것보다 작은 것이 회귀계수의 설명력을 높이게 된다(=회귀계수의 우연성(p-value)을 떨어뜨린다). a와 b값이 정확할수록 x에 대한 그 다음 y값을 보다 더 정확하게 예측해낼 수 있는 것처럼 말이다. 결국 회귀선을 기준으로 데이터의 분포가 조밀할 때, 우리는 표준오차는 작으면서 회귀계수와 추세선은 보다 정확할 것이라고 생각할 수 있다.

추세선은 얼마나 정확한 것일까, 회귀계수와 t-value
회귀분석은 기본적으로 독립변수와 종속변수 사이 양 또는 음의 상관관계가 전제돼야 한다. 그런데 만약 두 변수 간의 관계가 없다면, 다시 말해 기울기가 '0'이라면 애써 회귀분석을 실시한다 하더라도 아무런 의미가 없다. 회귀계수를 구하고 표준오차가 상대적으로 작다 할지라도 기울기(=변화)가 없다면, 예측할 근거가 전혀 없는 것과 같기 때문이다.
이쯤에서 다시 상기해야 할 점은 회귀선(=추세선)이 평균을 지나간다는 사실이다. 평균을 지나는 추세선의 기울기를 검정하는 방법으로 t-test를 활용하는데, 우린 1장에서 t-test는 두 자료의 차이를 평균과 표준편차의 비교로 설명한다는 내용을 배웠다. 그 가운데 데이터의 변동성은 표준편차(분산 참고)를 통해 설명 가능하므로 데이터의 변화 정도를 t-분포표를 참조하여 t-value를 확인(독립변수가 1개이므로 자유도는 '1'로 설정)하면 기울기가 '0'이 아닌 것을 확인함과 동시에 두 변수 관계 정도까지 확인할 수 있다.
회귀분석 결과표의 이해
수행한 회귀분석이 유의한 것이었는지 확인할 수 있는 분석 결과표다. 앞서 살펴보았듯 표준오차와 p값은 작을수록 추세선을 결정하는 회귀계수의 우연성이 낮아(=예측력이 높아)지며, t값은 커질수록 두 변수 간의 관계가 유의미하다는 것을 말해준다.

분석 연습
회귀분석은 보통 상관분석부터 시작된다. 상관관계를 계수로 확인하고 계숫값이 선형을 뜻할 때(1 또는 -1에 가까울 때) 회귀분석이 의미가 있다. 여기서는 청구금액(DMD_AMT)을 종속변수(y)로 설정하여 진료건수(DIAG_CNT), 입원일수(IPAT_DDNT), 상병건수(SICK_CNT), 약품목수(MITM_CNT)의 4가지 독립변수 후보 간 관계를 이해하고 회귀분석 시 가장 설명력이 높은 변수를 찾는다.
1) 771건의 샘플 데이터를 전처리한 뒤 선형의 관계를 찾기 위한 첫 번째 과정으로 그래프 대칭행렬의 시각화를 실시하여 분포를 확인한다. 점선 박스 처리된 그래프를 통해 선형적으로 설명될 수 있는 변수를 대략적으로 확인 가능하다.

2) 어떤 그래프가 선형적으로 관계 설명이 원활할지 그렇지 않은지를 독립변수 간 상관계수를 통해 더 정확히 알 수 있다.
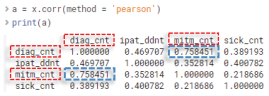
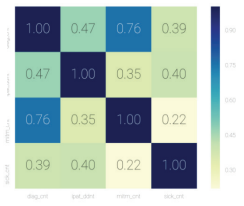
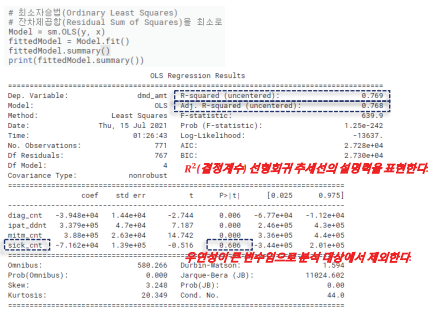
3) Statsmodels에서 OLS 함수를 실행하여 데이터 요약을 확인한다. 요약표 R-squared, P값을 통해 모델의 예측력과 유의수준을 확인한다. 상병건수가 유의수준이 0.6을 넘어가므로 모집단과 표본 간 평균이 다를 수 있다. 따라서 해당 변수는 제거해야 한다.
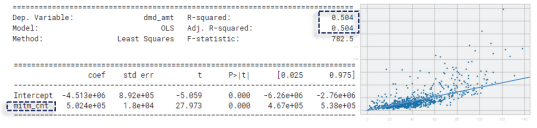
4) 상병건수를 제외한 나머지 세 변수와 청구금액과의 관계를 산점도와 함께 OLS 결과표로 확인한다. 3가지 변수 가운데 약품건수가 청구금액과의 상관계수를 비롯하여 추세선의 신뢰도(=설명력)가 가장 높아 청구금액의 크기에 가장 영향력 높은 변수로 확인됐다.
비선형회귀분석(Non-linear regression)
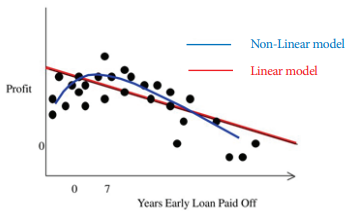
비선형회귀란 직선의 회귀선을 곡선으로 변환해 보다 더 정확하게 데이터 변화를 예측하는 데 목적이 있다. 현실에서의 데이터는 대개 선형보다 비선형적으로 더 상세하게 표현될 수 밖에 있다. 아래 그림에서 붉은색 선은 앞서 보았던 OLS 방식으로 데이터 산포를 회귀직선으로 설명한 것인데, 직선의 회귀선으로 y축의 이익이 감소 추세라는 사실은 설명할 수 있지만, 더욱 정확하게 데이터 변화를 예측하긴 어렵다.
그 이유는 직선의 회귀선이 곡선에 비해 '잔차'가 더 크기 때문이다. 잔차가 크다는 것은 실측과 추세선 사이의 표준오차가 크다는 의미를 내포하기 때문에 보다 정밀한 예측에 한계가 있다. 앞에서 우리는 표준 오차가 클수록 회귀계수의 우연성이 크다고 배웠다. 비선형 회귀식은 상대적으로 더 작은 잔차를 이용해 데이터 변화의 추세를 더욱 정교하게 설명할 수 있게 된다.
비선형은 현실과 맞닿아 있는 만큼 그 종류와 활용 케이스가 매우 다양하다. 따라서 본 포스팅에서는 여러 비선형 모델 가운데 분류에 주로 사용되는 로지스틱 회귀분석을 비선형 기법을 대표해 살펴보고자 한다.
함께 보면 좋은 글
[빅데이터분석기사] 로지스틱 회귀분석(Logistic Regression Analysis)
[빅데이터분석기사] 로지스틱 회귀분석(Logistic Regression Analysis)
로지스틱 회귀 데이터가 어떤 범주에 속할 확률을 0에서 1 사이의 값으로 예측하고, 그 확률에 따라 가능성이 더 높은 범주에 속하는 것으로 분류하는 기법이다. 0.5 보다 크면 어떤 사건이 일어
it-utopia.tistory.com
[빅데이터분석기사] 시계열분석(Time-series Analysis)
[빅데이터분석기사] 시계열분석(Time-series Analysis)
시계열분석 시간에 따라 변화되는 자료의 패턴을 밝혀 가까운 미래를 예측하는 방법이다. 시계열분석을 위해서는 시계열 데이터가 준비돼야 한다. 시간의 경과만 한 축(x)을 구성하는 것이 아니
it-utopia.tistory.com
[빅데이터분석기사] 최근접 이웃(K-Nearest Neighbors)
[빅데이터분석기사] 최근접 이웃(K-Nearest Neighbors)
최근접 이웃 알고리즘은 우리가 예측하려고 하는 임의의 데이터와 가장 가까운 데이터 K개를 찾아 다수결에 의해 데이터를 예측하는 방법이다. 위 그림과 같이 두 그룹의 데이터가 있을 때 주어
it-utopia.tistory.com
[빅데이터분석기사] 의사결정나무(Decision Tree)
[빅데이터분석기사] 의사결정나무(Decision Tree)
의사결정나무 일종의 분류 기법이다. 전체 집단을 계속 양분하는 분류기법으로써 분기가 발생하는 포인트(=노드)에는 기준이 되는 질문이 있어 기준 질문에 부합하냐(YES), 부합하지 않느냐(NO)에
it-utopia.tistory.com
[빅데이터분석기사] 랜덤포레스트(Random Forest)
[빅데이터분석기사] 랜덤포레스트(Random Forest)
랜덤포레스트(RF) 의사결정나무를 여러개 모아서 데이터 분류 및 예측을 수행하는 AI알고리즘이다. 어떤 데이터 집단에 대한 분류나 예측을 실시한다고 할 때, 하나의 결정트리를 사용하는 것보
it-utopia.tistory.com
'빅데이터분석기사 > 개념' 카테고리의 다른 글
| [빅데이터분석기사] 시계열분석(Time-series Analysis) (0) | 2022.05.28 |
|---|---|
| [빅데이터분석기사] 로지스틱 회귀분석(Logistic Regression Analysis) (0) | 2022.05.27 |
| [빅데이터분석기사] 주성분분석(Principal Component Analysis) (0) | 2022.05.25 |
| [빅데이터분석기사] 상관분석(Correlation Analysis) (0) | 2022.05.24 |
| [빅데이터분석기사] 분산분석(Analysis of Variance, ANOVA) (0) | 2022.05.23 |