서포트벡터머신(SVM)
분류를 위한 기준선을 정의하는 모델이다. 분류되지 않은 새로운 점이 나타나면 어느 쪽에 속하는지 확인을 위해서 결정 경계를 정한다.

데이터에 2개 속성(feature)만 있다면 결정 경계는 간단한 선 형태가 된다. 속성이 3개가 되면 3차원으로 그려야 한다. 이때의 결정 경계는 '선'이 아닌 '평면'이 된다. 우리가 이렇게 시각적으로 인지할 수 있는 범위는 딱 3차원까지다. 차원, 즉 속성의 개수가 늘어날수록 당연히 복잡해질 것이다. 결정 경계도 단순한 평면이 아닌 고차원이 되는데 이를 '초평면(hyperplane)'이라고 부른다.
결정 경계는 여러 형태로 정할 수 있다. 그래프C를 보면 경계선이 파란색 클래스(분류)와 너무 가까워 보인다. 결정 경계가 가장 적절한 것은 그래프 F다. 두 클래스 사이에서 거리가 가장 멀기 때문이다. 결정 경계는 데이터 군으로부터 최대한 멀리 떨어지도록 설정하는 것이 좋다.

마진(Margin)의 이해
마진(Margin)은 결정 경계와 서포트 벡터 사이의 거리를 의미한다.

위의 왼쪽 그림에서 직선 B1과 B2 모두 두 클래스를 무난하게 분류하고 있음을 확인할 수 있다. 좀 더 나은 결정경계를 꼽으라면 B1일 것이다. 두 범주를 여유 있게 구분하고 있다. b11을 plus-plane, b12를 minus-plane, 이 둘 사이의 거리가 마진(margin)이다. 결정 경계에 가장 가까운 각 클래스의 점들(데이터 포인트들)을 서포트벡터(support vectors)라 한다. 마진의 결정에 영향을 끼치는 관측치들로써, 이 데이터들이 경계를 정의하는 결정적인 역할을 한느 셈이다. SVM은 이 마진을 최대화하는 분류 경계면을 찾는 기법이라 할 수 있다.

경계면을 도식적으로 나타내면 위의 왼쪽 그림과 같다. 도식화된 분류 경계면을 w^T+b 이라고 할 때 벡터 w는 이 경계면과 수직인 법선벡터가 되며, 오른쪽 그림과 같이 마진의 폭은 2/||w|| 으로 정의된다. 마진의 폭이 최대가 되려면 벡터 w가 최소가 되어야 한다.
이상치(극단값, outlier)
이상치는 '패턴에서 벗어난 값' 또는 '중심에서 많이 벗어난 값'을 의미한다. 통계적 자료 분석의 결과를 왜곡시키거나 자료 분석의 적절성을 위협하는 변숫값을 뜻하기도 한다.

왼쪽에 혼자 떨어져 있는 파란 점과, 오른쪽에 혼자 떨어져 있는 빨간 점이 이상치이다.
위쪽 그림은 서포트 벡터와 결정 경계 사이의 거리가 매우 좁아져서 마진이 매우 작아진 상태이다. 이런 상태를 하드 마진(hard margin)이라고 한다. 이상치를 허용하지 않는 기준으로 결정 경계를 정해버리면 과대적합(overfitting) 문제가 발생할 수 있다.
아래쪽 그림은 이상치들이 마진 안에 어느 정도 포함되도록 기준을 잡았다. 서포트 벡터와 결정 경계 사이의 거리가 멀어져서 마진이 커진 상태이다. 이런 상태를 소프트 마진(soft margin)이라고 한다. 이 경우 과소적합(underfitting) 문제가 발생할 수 있다.
문제정의
분리된 두 클래스를 선형으로 가장 적절하게 결정 경계를 정하도록 하자.
DATASET
각 클래스를 구분하기 위해 'O'와 'X'로 데이터를 표시하고, 'O'는 '-1 class'로, 'X'는 '+1 class'로 구분하여 표시한다. 샘플데이터는 각 클래스당 20개로 설정한다.
from sklearn.datasets import make_bolbs
X, y = make_bolbs(n_samples=40, centers=2, cluster_std=0.5, random_state=4)
y = 2*y-1
plt.scatter(X[y == -1, 0], X[y == -1, 1], marker='o', label="-1 class")
plt.scatter(X[y == +1, 0], X[y == +1, 1], marker='x', label="+1 class")
plt.xlabel("x1")
ply.ylabel("x2")
plt.legend()
plt.title("SVM sample")
plt.show()import numpy as np
from sklearn.sym import SVC
model = SVC(kernel='linear', C=1e10).fit(X, y)
xmin = X[:, 0].min()
xmax = X[:, 0].max()
ymin = X[:, 1].min()
ymax = X[:, 1].max()
xx = np.linspace(xmin, xmax, 10)
yy = np.linspace(ymin, ymax, 10)
...
plt.scatter(X[y == +1, 0], X[y == +1, 1], marker = 'x', label = "+1 class")
plt.contour(X1, X2, Z, levels, colors='k', linestyles=linestyles)
plt.scatter(model.support_vectors_[:, 0], model.support_vectors_[:, 1], s=300, alpha=0.3)
x_new = [10, 2]
plt.scatter(x_new[0], x_new[1], marker='^', s=100)
plt.text(x_new[0], x_new[1] + 0.08, "Test Data")
plt.xlabel("x1")
plt.ylabel("x2")
plt.legend()
plt.title("SVM Predict Result")
plt.show()
문제정의
분리된 두 클래스가 비선형인 경우 결정 경계를 정하도록 하자.
DATASET
데이터 등 관련 자료와 설명
- 하나의 클래스는 '□', 다른 클래스는 '△'로 구분하여 표시한다. 커널은 다항식(poly)을 사용한다.
import numpy as np
from matplotlib pyplot as plt
def plot_dataset(X, y, axes):
plt.plot(X[:, 0][y==0], X[:, 1],[y==0], "bs")
plt.plot(X[:, 0][y==1], X[:, 1],[y==1], "g^")
plt.axis(axes)
plt.grid(True, which='both')
plt.xlabel(r"$x_1$", fontsize = 20)
plt.ylabel(r"$x_2$", fontsize = 20, rotation = 0)
def plot_predictions(df, axes):
x0s = np.linspace(axes[0], axes[1], 100) # axes[0]부터 axes[1]까지 100개로 이루어진 숫자들
x1s = np.linspace(axes[2], axes[3], 100)
x0, x1 = np.meshgrid(x0s, x1s) # 표현할 수 있는 모든 배열조합
X = np.c_[x0.ravel(), x1.ravel()] # ravel 1차원 배열로 핀다
y_pred = clf.predict(x).reshape(x0.shape)
y_decision = clf.decision_function(X).reshape(x0.shape)
plt.contourf(x0, x1, y_pred, cmap=plt.cm.brg, alpha=0.2)
plt.contourf(x0, x1, y_decition, cmap=plt.cm.brg, alpha=0.1)
# 다항식(polynomial) 커널을 사용하면 데이터를 더 높은 차원으로 변형하여 나타냄으로써 초평면(hyperplane)의 결정 경계를 얻을 수 있다.
plot_predictions(polynomial_scm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, Y, [-1.5, 2.5, -1, 1.5])
plt.show()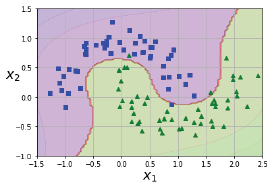
from sklearn.svm import SVC
poly_kernel_scm_clf = Pipeline([
("scaler", StandardScaler())
("svm_clf", SVC(kernel="poly", degree=3, coef0=1, C=5))
])
# coef0는 모델이 높은 차수와 낮은 차수에 얼마나 영향을 끼치는지 정할 수 있다.
poly_kernel_svm_clf.fit(X, Y)
plt.figure(figsize=(11, 4))
plt.subplot(121)
plot_predictions(poly_kernel_svm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, Y, [-1.5, 2.5, -1, 1.5])
plt.title(r"$d=3, r=1, C=5$", fontsize=18)
poly_kernel_svm100_clf = Pipeline([
("scaler", StandardScaler()),
("svm_clf", SVC(kernel="poly", degree=10, coef0=100, C=5))
])
poly_kernel_svm100_clf.fit(X, Y)
plt.subplot(122)
plot_predictions(poly_kernel_scm100_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, Y, [-1.5, 2.5, -1, 1.5])
plt.title(r"$d=10, r=100, C=5$", fontsize=18)
plt.show()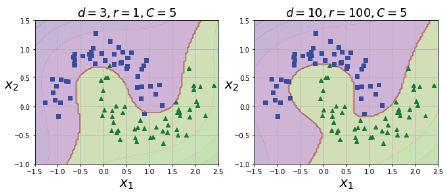
매개변수인 coef()값을 1에서 100으로 변경할 경우 결정 경계가 오른쪽 그림과 같이 달라짐을 알 수 있다.
함께 보면 좋은 글
[빅데이터분석기사] 군집분석(Clustering Analysis)
[빅데이터분석기사] 군집분석(Clustering Analysis)
군집분석 분류 기준이 없는 상태에서 데이터 속성을 고려해 스스로 전체 데이터를 N개의 소그룹으로 묶어내는(Clustering) 분석법이다. 유사성이 높은 대상 데이터를 묶고, 서로 다른 그룹에 속한
it-utopia.tistory.com
[빅데이터분석기사] 인공신경망(Artificial Neural Network)
[빅데이터분석기사] 인공신경망(Artificial Neural Network)
핵심요약 인공신경망(ANN)은 기계학습과 인지과학 분야에서 고안한 학습 알고리즘이다. 신경세포의 신호 전달체계를 모방한 인공뉴런(노드)이 학습을 통해 결합 세기를 변화시켜 문제를 해결하
it-utopia.tistory.com
[빅데이터분석기사] 심층신경망(Deep Neural Network)
[빅데이터분석기사] 심층신경망(Deep Neural Network)
핵심요약 심층신경망(Deep Neural Network)은 인공신경망(Aritificial Neural Network)과 동일한 구조와 동작 방식을 갖고 있다. 심층신경망은 단지 인공신경망에서 은닉층(Hidden Layer)의 깊이가 깊어진 형태를
it-utopia.tistory.com
[빅데이터분석기사] 합성곱신경망(Convolutional Neural Network)
[빅데이터분석기사] 합성곱신경망(Convolutional Neural Network)
핵심요약 합성곱신경망(CNN)은 인공신경망 모델의 하나로 패턴을 찾아 이미지를 분석하는데 특화된 알고리즘이다. 주요 구성은 크게 합성곱(Convolution) 연산과 풀링(Pooling) 연산으로 나눌 수 있다.
it-utopia.tistory.com
[빅데이터분석기사] 순환신경망(Recurrent Neural Network)
[빅데이터분석기사] 순환신경망(Recurrent Neural Network)
핵심요약 순환신경망(Recurrent Neural Network)은 시간 순서가 있는 데이터를 잘 예측하도록 설계된 인공신경망 모델들 중 하나이다. 과거의 신호를 기억할 수 있는 장치(Hidden State)를 두어 입력신호를
it-utopia.tistory.com
'빅데이터분석기사 > 개념' 카테고리의 다른 글
| [빅데이터분석기사] 인공신경망(Artificial Neural Network) (0) | 2022.06.09 |
|---|---|
| [빅데이터분석기사] 군집분석(Clustering Analysis) (0) | 2022.06.08 |
| [빅데이터분석기사] 앙상블(Ensemble) (0) | 2022.06.04 |
| [빅데이터분석기사] 랜덤포레스트(Random Forest) (0) | 2022.06.02 |
| [빅데이터분석기사] 의사결정나무(Decision Tree) (0) | 2022.05.30 |