[빅데이터분석기사] 인공신경망(Artificial Neural Network)

핵심요약

 

  인공신경망(ANN)은 기계학습과 인지과학 분야에서 고안한 학습 알고리즘이다. 신경세포의 신호 전달체계를 모방한 인공뉴런(노드)이 학습을 통해 결합 세기를 변화시켜 문제를 해결하는 모델 전반을 가리킨다.

 

신경세포                                                                         퍼셉트론

 

인공신경망의 시작, 퍼셉트론

 

  퍼셉트론은 신경세포 뉴런들이 신호, 자극 등을 받아 어떠한 임계값(threshold)을 넘어서면 그 결고를 전달하는 신경세포의 신호 전달 과정을 착안하여 만들어졌다. 이를 수학적인 기호로 모델링 한 것이 퍼셉트론인데, 퍼셉트론은 각각의 가중치의 크기를 적절히 조절하여 입력 신호이 크기를 정한다. 입력 신호들의 합에 활성화 함수를 거쳐 나온 결괏값을 전달함으로써 원하는 결괏값을 얻는 방식으로 동작한다.

 

  아래 그림은 단층 퍼셉트론으로 AND, OR, NAND와 같은 비교적 간단한 문제를 해결할 수 있는 예시이다. 입력값에 대해 정해진 결괏값을 출력할 수 있는 가중치의 경우의 수는 무수히 많으며(퍼셉트론 그림에서 출력 식 참고), 주어진 연산을 만족하는 가중치의 조합을 찾음으로써 문제를 푼다고 할 수 있다.

 

단층 퍼셉트론에서 AND, OR, NAND 문제 및 가중치 예시

 

단층 퍼셉트론의 한계

 

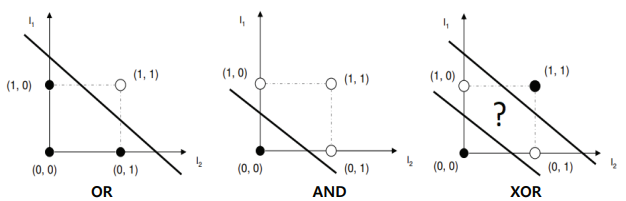
  앞서 살펴본 단층 퍼셉트론으로 AND, OR, NAND(=NOT AND)와 같은 비교적 단순한 논리 게이트는 구현할 수 있었지만 XOR같은 문제를 풀 수 없는 한계가 있었다. 이는 좌표평면상에 결정 경계(Decision Boundary)를 그어보면 좀 더 복잡한 문제를 해결할 수 있다는 것을 발견하였다. 현재 다양한 종류의 인공신경망은 모두 입력측, 은닉층, 출력층으로 나누어 구성된다.

 

 

다층 퍼셉트론의 등장

 

  이와 같은 문제를 해결하기 위해 다층 퍼셉트론이 등장하였다. NAND와 OR연산의 결괏값을 다시 AND하여 XOR연산을 표현할 수 있다는 점에서, 입력층과 출력층 사이에 은닉층을 두어 다층 퍼셉트론을 만들면 좀 더 복잡한 문제를 해결할 수 있다는 것을 발견하였다. 현재 다양한 종류의 인공신경망은 모두 입력층, 은닉층, 출력층으로 나누어 구성된다.

 

 

활성화 함수(Activation Function)

 

  앞서 살펴본 것처럼 은닉층을 여러 층 두면 단순한 선형이 아니라 좀 더 복잡한 분류기를 만들 수 있는 가능성을 보았다. 하지만 단순히 은닉층(Hidden Layer)을 쌓는 것만으로는 부족하다. 왜냐하면 출력값이 다음 입력값으로 넘어갈 때 선형식(Linear)으로 전파된다면 은닉층 여러 개 두는 방식이나 하나를 두는 것이나 차이가 없기 때문이다. 이러한 이유로 출력층의 결괏값을 비선형(Non Linear)으로 변환시켜 줄 장치인 '활성화 함수(Activation Function)'를 두게 되었다.

 

  인공신경망에는 다양한 활성화 함수(Activation Function)가 존재한다. 대표적으로 Sigmoid, Tanh, ReLU 등이 있다. Sigmoid의 경우 양 끝에서 기울기가 거의 0에 수렴하고, 이로 인한 기울기 소실(Vanishing Gradient) 문제가 생기기 때문에 대부분 인공신경망은 활성화 함수로 ReLU 함수를 사용한다.

 

  ReLU 함수는 0보다 작은 구간에서 기울기가 0이고 나머지 0보다 큰 구간에서는 항상 일정한 크기의 기울기 소실 문제를 막아 좋은 학습 결과를 기대할 수 있다.

 

  활성화 함수는 인공신경망이 학습을 잘할 수 있도록하는 하나의 수학적 장치이며 모델 설계 시 다양하게 실험하여 좋은 것을 선택하면 된다.

 

활성화 함수와 도함수의 그래프

 

활성화 함수가 비선형인 이유?

  f(x) = cx 일 때, 은닉층이 3개라면 3개 층을 거친 결괏값은 f(f(f(x)))이 될 것이고 이는 g(x) = cx^3인 하나의 은닉층과 같은 결과이므로 은닉층을 여러 개 둔 효과를 기대하기 어렵다.

 

 

학습(Learning)

 

  다층 퍼셉트론으로 좀 더 어려운 문제도 풀 수 있다는 것을 알게 되었지만 아직 중요한 부분이 남아있다. 바로 학습이다. 아직까지는 입력값에 원하는 결괏값이 나올 수 있도록, 적절한 가중치를 사람이 직접 넣었기 때문에 학습을 한다고 할 수 없다. 학습을 위해서는 인공신경망이 데이터를 잘 표현(Representation)하도록 무수히 많은 가중치들의 조합을 스스로 찾을 수 있는 과정 및 장치들이 필요하다. 인공신경망이 학습하는 과정을 알아보자.

 

 

손실 함수(Loss Function)

 

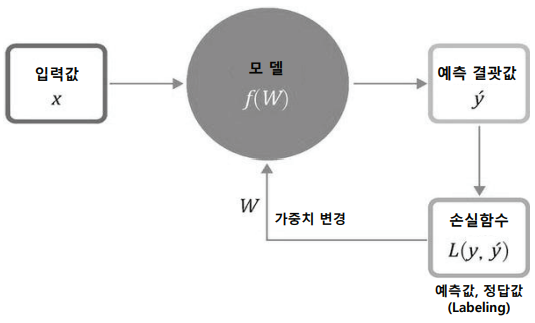
  인공신경망이 수많은 학습데이터를 이용하여 모델을 잘 표현하기 위해서는 입력데이터에 대한 결괏값(Output)이 원하는 정답값(Labeling)과 얼마나 다른지 끊임없이 피드백(Feedback)하는 과정이 필요하다. 손실 함수는 바로 이 과정에서 학습데이터가 모델(입력층->은닉층->출력층)을 통해 나온 결괏값이 실제로 우리가 원하는 값(Labeling)과 얼마나 다른지 정도를 측정하기 위해 사용하는 함수를 말하며 이를 토대로 가중치를 변경하게 된다. 같은 의미로 비용함수(Cost Function)라고 표현하기도 한다.

 

  손실 함수(Loss Function)은 문제의 유형에 따라 대표적으로 평균제곱오차(Mean Squared Error)와 교차엔트로피 오차(Cross Entropy Error)가 있는데, 두 가지 모두 입력에 대한 예측값(Prediction)과 정답값(Labeling)이 비슷할수록 작은 값이 나오게 설계되어 있다.

 

학습 : 손실함수를 통한 가중치 변경

 

가중치 변경

 

  딥러닝 분야의 세계적인 권위자이자 페이스북 AI연구 이사 얀 르쿤(Yann LeCun) 교수는 신경망이 가중치의 조합을 찾는 것(학습)을 최적의 소리를 찾기 위해 음향장치의 수많은 조절기의 상태를 기계 스스로 찾는 것에 비유하기도 하였다. 그렇다면 이 조절기는 어떤 방법으로 조절하고 찾을 수 있을까?

 

얀 르쿤(Yann LeCun) 교수                                                         음향기기(Sound Control Mixer)

 

 

순전파(Feedforward), 역전파(Backpropagation), 최적화(Optimization)

 

  앞에서 인공신경망이 수많은 가중치를 변경하여 데이터를 잘 표현하는 가중치를 찾아 문제를 해결하며, 가중치를 변경할 때 참고하는 도구로써 손실 함수(Loss Function)를 사용한다는 것을 살펴보았다.

  그렇다면 우리의 고민은 이렇게 정리할 수 있다. '어떻게 하면 손실 함수(Loss Fucntion)의 값을 최소로 만들 수 있을까?(예측값과 정답값을 비슷하게 하는 가중치의 조합을 찾기)' 인공신경망은 최적화(Optimization)와 역전파(Backpropagation)의 방식을 이용한다. 손실 함수가 각각의 가중치를 변수로 하는 함수라는 점을 이용하여, 손실 함수의 값을 각각 가중치들로 국소적 미분하고 지역적 최솟값(Local Minimum)으로 하는 가중치들을 찾는다. 이때 가중치는 연쇄 법칙(Chain Rule)을 사용하여 역전파(Backpropagation)법으로 최솟점을 찾는 기울기 하강(Gradient Descent)을 하며 변경(Updata)된다.

 

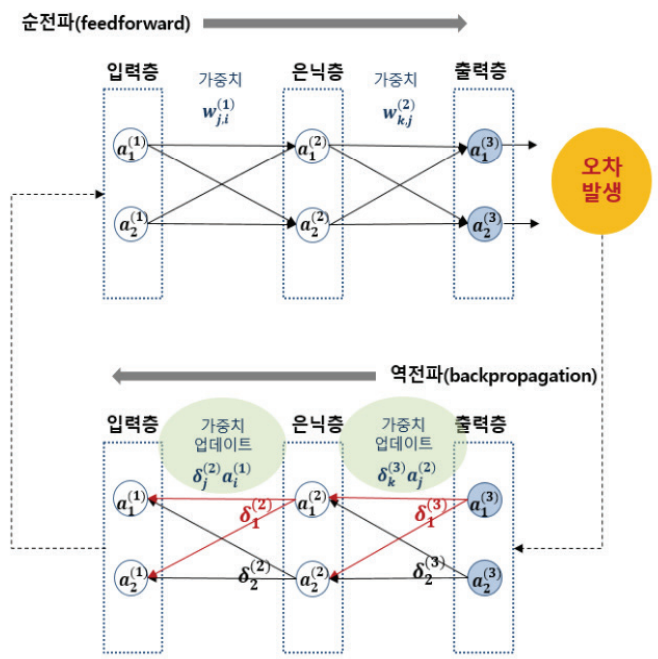
  인공신경망은 모델이 예측 결괏값을 찾는 과정이 입력층-은닉층-출력층으로 순차적으로 흐른다고 하여 순전파(Feedforward)라 하며 가중치의 수정은 출력층-은닉층-입력층으로 흐르기 때문에 역전파(Backpropagation)라고 한다. 또한 최적의 가중치를 찾아가는 방식, 그러한 알고리즘을 최적화(Optimization)라고 한다.

 

순전파(Feedforward)와 역전파(Backpropagation)

 

역전파(Backpropagation) 이해하기

 

  사과의 최종 가격이 어떤 요소에 의해서 영향을 받는다고 하자. 만약 다른 요소를 통제한 상태에서 하나의 요인이 최종 사괏값에는 어떠한 영향을 끼치는지 알고자 할 때, 다음과 같이 계산 그래프를 그려 결과를 도출할 수 있다.

 

 

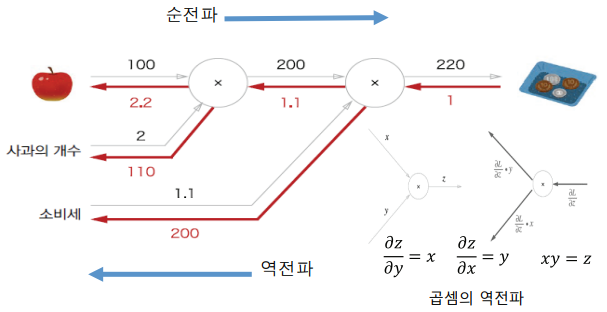
1) 주어진 식(사과 단가, 개수, 소비세)에 따라 계산 그래프를 구성한다.

2) 그래프에서 계산을 왼쪽에서 오른쪽으로 진행한다. : 100원*2개*1.1 = 220원

3) 국소적 미분값을 표현하여 단계마다 표시한다.

4) 각 요소(단가, 개수, 소비세)에 대한 영향도의 크기를 계산한다.

 

  100원짜리 사과 2개가 소비세 10%를 더해 22원이라고 할 때, 우리는 계산 그래프를 통해 다음과 같이 해석할 수 있다. 사과가 1원 오르면 최종 금액은 2.2원 오르고, 사과의 개수가 하나 더 생길 때마다 총액은 110원이 오른다. 즉, 각 요소들이 총 금액에 대해 얼마만큼 영향을 끼치는지 알 수 있는 것이다.

 

  이를 인공신경망에 적용하면 수많은 각각의 가중치의 값을 편미분(Partial Derivative)하여 비용함수(Cost Function)로부터 발생하는 값이 최소가 되는 가중치값을 구할 수 있고, 이는 결과적으로 데이터를 가장 잘 표현(Representation)하는 모델을 만드는 것이 된다.

 

 

함께 보면 좋은 글

 

[빅데이터분석기사] 심층신경망(Deep Neural Network)

[빅데이터분석기사] 심층신경망(Deep Neural Network)

 

[빅데이터분석기사] 합성곱신경망(Convolutional Neural Network)

[빅데이터분석기사] 합성곱신경망(Convolutional Neural Network)

 

[빅데이터분석기사] 순환신경망(Recurrent Neural Network)

[빅데이터분석기사] 순환신경망(Recurrent Neural Network)

 

[빅데이터분석기사] 연관규칙분석(Association Rule Analysis)

[빅데이터분석기사] 연관규칙분석(Association Rule Analysis)

 

[빅데이터분석기사] 교차분석(Cross-tabulation Analysis)

[빅데이터분석기사] 교차분석(Cross-tabulation Analysis)