로지스틱 회귀
데이터가 어떤 범주에 속할 확률을 0에서 1 사이의 값으로 예측하고, 그 확률에 따라 가능성이 더 높은 범주에 속하는 것으로 분류하는 기법이다.
0.5 보다 크면 어떤 사건이 일어난다.(성공확률)
0.5 보다 작으면 어떤 사건이 일어나지 않는다.(실패확률)

합격/불합격, 성공/실패, 생존/사망, 진실/거짓 등 이분법적인 결과를 도출하기 위해 주로 사용되는 회귀분석 방식으로 예측을 주목적으로 하는 회귀분석과 차이가 있다.
로지스틱 회귀분석 방법
로지스틱 회귀 분석은 이진 분류를 수행한믄 데 사용된다. 즉, 데이터 샘플을 양성(1) 또는 음성(0) 클래스 둘 중 어디에 속하는지 예측한다. 각 속성(feature)들의 계수 log-odds를 구한 후 시그모이드 함수를 적용하여 실제로 데이터가 해당 클래스에 속할 확률을 0과 1사이의 값으로 나타낸다.
오즈비(Odds Ratio)
오즈비는 사건이 발생할 확률이 발생하지 않을 확률에 비해 몇 배 더 높은가를 설명하는 개념이다.
P(성공확률) = 사건 발생함, 1-P(실패확률) = 사건 발생X

A : 97명 - 코로나 환자와 접촉 후, 코로나에 감염됨
B : 307명 - 코로나 환자와 접촉 후, 코로나에 감염되지 않음
C : 200명 - 코로나 환자와 접촉하지 않았지만, 코로나에 감염됨
D : 1409명 - 코로나 환자와 접촉하지 않았고, 코로나에 감염되지 않음
Odds Ratio(OR) = 136674/61400 = 2.2로 계산된다.
따라서, 코로나 환자와 접촉한 사람은 접촉하지 않은 사람보다 코로나 감염이 될 가능성이 2.2배 높다고 할 수 있다.
로짓(logit) 변환 : 오즈비에 log 함수 적용한 것으로 로짓을 대상으로 회귀분석을 적용한 것이 로지스틱 회귀분석이 된다.
logit = log(p/1-p)
문제정의
N대학교의 대학원 입학처는 본교 대학원에 입학하는 학생이 어떠한 특성을 가지는지 파악하고 대학원에 입학할 가능성이 있는 수험생을 예측하고자 한다. 입시점수와 학점이 합격여부에 어떤 영향이 있는지를 확인한다.
DATASET : 데이터 등 관련 자료와 설명
# 합격여부, 입시점수 및 학점에 대한 정보를 test.csv로 저장한다.
import pandas as pd
import numpy ad np
import statsmodel.api as sm
import matplotlib.pyplot as plt
## 사이킷런(sklearn) 패키지 이용
from sklearn import dataset
from sklearn import metrics
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score, roc_auc_score, roc_curve
data = pd.read_csv('./Logistic Regression/test.csv', encoding = 'cp949')
data.head()
분석
# 독립변수와 종속변수를 지정해주고 훈련용 데이터와 검증용 데이터를 7:3으로 분할해준다.
## 변수 지정
x = data[['입시점수', '학점']] # 독립변수
y = data[['합격여부']] # 종속변수
## 학습데이터와 평가(test)데이터 분리
## rendom_state는 난수 생성 프로그램을 사용할 때 사용한다. 기본값은 없다.
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=0)
from sklearn.linear_model import LogisticRegression
## 로지스틱 회귀분석 모델 생성
model = LogisticRegression()## 모델의 정확도 확인
model.fit(x_train, np.ravel(y_train))
print('학습용 데이터 세트 정확도 : %.2f' % model.score(x_train, y_train))
print('검증용 데이터 세트 정확도 : %.2f' % model.score(x_test, y_test))
# 조금 더 자세한 평가를 위해 classification_report 모듈을 이용한다. 이 모듈은 모형 성능평가를 위한 모듈로 정밀도(precision), 재현율(recall), F1-score, support를 구해준다.
from sklearn.metrics import classification_report
y_pred=log.predict(x_test)
print(classification_report(y_test, y_pred)
이제 모델의 회귀계수와 오즈비를 구해 독립변수가 분류 결정에 미치는 영향의 정도를 알아보기 위해 다른 방식의 로지스틱 회귀분석을 진행해보자. logit이란 변수에 합격 여부를 종속변수로 하는 데이터를 넣고, 앞서 넣은 독립변수 x값도 입력한 뒤 적합 시켜준다.
# 로지스틱 회귀분석 연습
train_cols = data.columns[1:] ## train_cols는 독립(설명)변수
logit = sm.Logit(data[['합격여부']].x)
## result = logit.fit()
## 로지스틱 회귀모델을 적합 시킬 때에 사용하는 최적화 기법 지정
result = logit.fit(method = 'newton')
정밀도 : 모델이 True라고 분류한 것 중에서 실제 True인 것의 비율이다.
e.g.) 날씨 예측 모델이 맑다로 예측했는데, 실제 날씨가 맑았는지를 살펴보는 지표
재현율 : 실제 True인 것 중에서 모델이 True라고 예측한 것의 비율이다.
e.g.) 실제 날씨가 맑은 날 중에서 모델이 맑다고 예측한 비율을 나타낸 지표
# 회귀계수확인
result.params
# summary 함수로 결과 확인
result.summary2()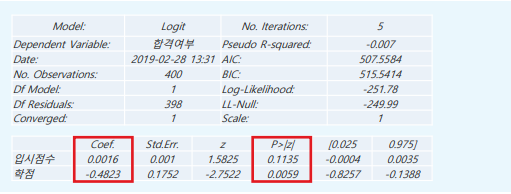
각 회귀계수가 합격 여부에 어떻게 영향을 미치는지 확인한다. 먼저, 유의확률(P>|z|) 즉 P-value를 본다. P-value의 기본값인 0.05 이하인 경우 유의미한 값으로 보기 때문에 학점 변수가 종속변수에 영향을 주는 유의미한 변수임을 알 수 있다. 입시점수를 제외하고 계속해서 해석을 진행한다. 편회귀계수(Coef.)의 부호를 통해 종속변수에 미치는 영향을 차악할 수 있다. 편회귀계수(Coef.)의 값이 양수라면 합격여부가 '1'일 확률이 높아진다는 뜻이다. 반대로 음수라면 합격 여뷰의 값이 '0'일 확률이 높아진다는 뜻이다. 따라서 모형의 회귀계수 분석결과는 다음과 같다. 통계량에 나와있는 편회귀계수의 값 자체만으로는 각 변수들이 종속변수에 얼마나 영향을 주는지는 파악할 수 없다.
- 유의확률 : 유의확률(p-value, p값)은 귀무가설이 진실일 때 적어도 그 정도의 극단적인 표본값이 나올 확률, 즉 귀무가설이 참임에도 이를 기각할 확률
- 유의수준 : 유의수준은 귀무가설의 기각여부를 결정하는데 사용하는 기준이 되는 확률
- 귀무가설 : 설정한 가설이 진실일 확률이 극히 적어 처음부터 버릴 것이 예상되는 가설
- 편회귀계수 : 회귀식에 포함되는 다른 변수의 영향을 제거한 후 독립변수가 종속변수에 주는 영향을 나타낸다. 원인(독립변수)이 여러 개인 다중회귀분석에서의 회귀계수를 의미
# 종속변수에 미치는 정도느 오즈비(Odds Ratio, 승산비)를 통해 파악할 수 있다.
# 다음과 같은 코드를 작성해서 오즈비를 구해보자.
np.exp(result.params)
오즈비가 1을 기준으로 큰지 작은지를 파악하여 종속변수에 미치는 영향의 방향을 파악할 수 있다. 독립변수가 두개 이상 있을 때는 다른 독립변수를 일정한 값으로 고정한 경우의 오즈비로 해석된다. 아무런 관계가 없을 때 오즈비는 1이다. 1에서 멀리 떨어질수록 종속변수와의 관계가 강하다는 뜻이다. 즉, 종속변수 여부에 큰 영향을 준다는 뜻이다.
오즈비는 1을 기준으로 영향을 판단하므로, 오즈비가 10인 경우와 0.1인 경우는 종속변수에 영향을 주는 강도가 같다. 입시점수 변수의 경우, 극도로 1에 가까운 값으로 나타난다. 따라서, 입시점수는 합격여부에 별다른 영향을 주지 않았음(관계 없음)을 알 수 있다. 독립변수가 수치형일 경우 또 다르게 오즈비를 해석할 수 있다. 학점이 1단위 증가하면 합격할 확률이 0.61배 증가한다는 뜻으로도 해석할 수 있다. 따라서, 대학원 입학에는 입시점수보다 학점이 중요한 것을 알 수 있었다.
성능 확인
# cut_off 함수를 생성하여 임계치(threshold) 설정
# 로지스틱은 확률값을 표현하기 때문에 임계치를 정해줘야 함
# 일반적으로 임계치를 0.5로 정하여, 0.5 이상히면 1로, 아니면 0으로 판단
def cut_off(y, threshold):
Y = y.copy() # 대문자 Y를 새로운 변수로 지정하여 기존의 y값에 영향을 주지 않도록 함
Y[Y > threshold] = 1
Y[Y <= threshold] = 0
return(Y.astype(int))
pred_Y = cut_off(pred_y, 0.5)
# confusion_matrix 함수로 혼동행렬을 뽑는다.
cfmat = confusion_matrix(y_test, pred_Y)
print(cfmat)
# 혼동행렬의 결괏값으로 정확도를 구한다.
(cfmat[0,0] + cfmat[1,1] / np.sum(cfmat) ## accuracy
def acc(cfmat):
acc = (cfmat[0,0] + cfmat[1,1]) / np.sum(cfmat)
return(acc)
# cut_off 함수에 따른 성능지표 비교
# 임계치(threshold) 따라 성능이 달라질 수 있다.
# 조금씩 바꾸면서 성능이 어떻게 바뀌는지 확인
threshold = np.arange(0.1, 0.1)
table = pd.DataFrame(column = ['ACC'])
for i in threshold:
pred_Y = cut_off(pred_y, i)
cfmat = confusion_matrix(y_test, pred_Y)
table.loc[i] = acc(cfmat)
table.index_name = 'threshold'
table.columns.name = 'preformance'
table
정확도(ACC) 값이 가장 높은 부분의 임계치(threshold)가 성능이 가장 좋은 것으로 0.8 정도가 가장 성능이 좋게 나온 것을 알 수 있다.
Confusion_matrix(혼동행렬)
특정 분류 모델의 성능을 평가하는 지표로, 실젯값과 모델이 예측한 예측값을 한 눈에 알아볼 수 있게 배열한 행렬이다. 이진 분류의 경우 실젯값과 예측값을 참/거짓에 따라 분류한다.
# ROC, AUC로 해당 모델 검증
# sklearn ROC 패키지 이용
fpr, tpr, thresholds = metrics.roc_curve(y_test, pred_y, pos_label = 1)
# Print ROC Curve
plt.plot(fpr, tpr)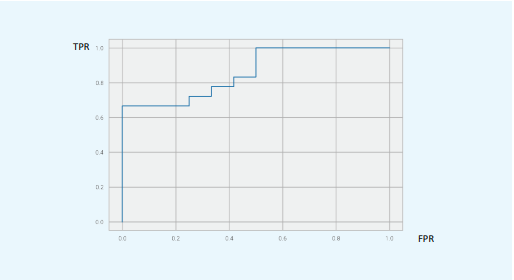
# Print AUC
auc = np.trapz(tpr, fpr)
print('AUC:', auc)
함께 보면 좋은 글
[빅데이터분석기사] 시계열분석(Time-series Analysis)
[빅데이터분석기사] 시계열분석(Time-series Analysis)
시계열분석 시간에 따라 변화되는 자료의 패턴을 밝혀 가까운 미래를 예측하는 방법이다. 시계열분석을 위해서는 시계열 데이터가 준비돼야 한다. 시간의 경과만 한 축(x)을 구성하는 것이 아니
it-utopia.tistory.com
[빅데이터분석기사] 최근접 이웃(K-Nearest Neighbors)
[빅데이터분석기사] 최근접 이웃(K-Nearest Neighbors)
최근접 이웃 알고리즘은 우리가 예측하려고 하는 임의의 데이터와 가장 가까운 데이터 K개를 찾아 다수결에 의해 데이터를 예측하는 방법이다. 위 그림과 같이 두 그룹의 데이터가 있을 때 주어
it-utopia.tistory.com
[빅데이터분석기사] 의사결정나무(Decision Tree)
[빅데이터분석기사] 의사결정나무(Decision Tree)
의사결정나무 일종의 분류 기법이다. 전체 집단을 계속 양분하는 분류기법으로써 분기가 발생하는 포인트(=노드)에는 기준이 되는 질문이 있어 기준 질문에 부합하냐(YES), 부합하지 않느냐(NO)에
it-utopia.tistory.com
[빅데이터분석기사] 랜덤포레스트(Random Forest)
[빅데이터분석기사] 랜덤포레스트(Random Forest)
랜덤포레스트(RF) 의사결정나무를 여러개 모아서 데이터 분류 및 예측을 수행하는 AI알고리즘이다. 어떤 데이터 집단에 대한 분류나 예측을 실시한다고 할 때, 하나의 결정트리를 사용하는 것보
it-utopia.tistory.com
[빅데이터분석기사] 앙상블(Ensemble)
앙상블 학습(Ensemble Learning) 그동안 우리는 여러 기계학습 모델들을 살펴보았다. 이렇게 개별적으로 동작하는 모델들을 모아 종합적으로 의사결정을 한다면 어떨까? 앙상블은 프랑스어로 전체적
it-utopia.tistory.com
'빅데이터분석기사 > 개념' 카테고리의 다른 글
| [빅데이터분석기사] 최근접 이웃(K-Nearest Neighbors) (0) | 2022.05.29 |
|---|---|
| [빅데이터분석기사] 시계열분석(Time-series Analysis) (0) | 2022.05.28 |
| [빅데이터분석기사] 회귀분석(Regression Analysis) (0) | 2022.05.26 |
| [빅데이터분석기사] 주성분분석(Principal Component Analysis) (0) | 2022.05.25 |
| [빅데이터분석기사] 상관분석(Correlation Analysis) (0) | 2022.05.24 |